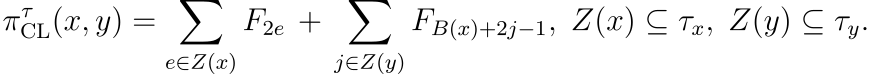We demonstrate (bellow) our carryless pairing constructed solely from addition and bounded recursion.

First, a chosen set of Fibonacci terms is aggregated into a single numerical value. In a second step, the selection itself is discarded, and only the resulting sum is returned to a greedy algorithm.

Remarkably, the original terms can be recovered from the sum alone. This round-trip—from arbitrary additive input to canonical Zeckendorf Representation and back—utilizes Binet’s Formula, Hurwitz’s Theorem, and Zeckendorf’s Theorem to yield a stable, reversible, and fully bounded encoding–decoding scheme.

The greedy structure can be used to realize an injective arithmetical pairing function: